圧縮性流体の全温全圧について - 機械系技術者の雑記帳

圧縮性流体の全温・全圧

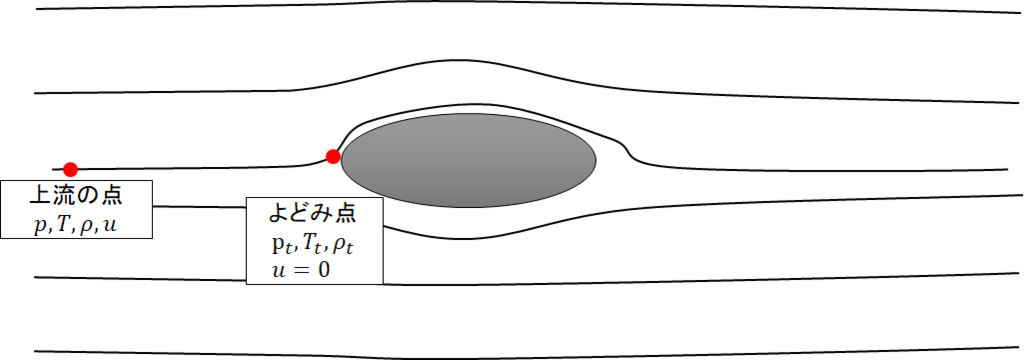
全温・全圧は高速気流が淀んだ点での温度・圧力のことで、全温は全温度(Total Temprature)やよどみ点温度(Stagnation Temperature)とも呼ばれ、全圧は全圧力(Total Pressure) とも呼ばれます。ある圧力、温度、流速を持つ流れが、もし淀んだ場合どういう状態になるかという量です。

f:id:tone_akadaya:20171208233708p:plain

（※以下、数式の描画に時間がかかる場合があります。）

全温の導出（理想気体）

単位質量あたりのエネルギー保存則

$\rm \frac{p}{ \rho } + C_v T +\frac{1}{2} u^2 = \frac{p_t}{ \rho_t} + C_v T_t$ 　…(1)

(p:圧力, ρ:密度, T:温度, u:流速, Cv:等積比熱)
左辺の、
第1項は周りの流体を押しのけているエネルギー、
第2項は温度による内部エネルギー、
第3項は運動エネルギー、
右辺の添字t付きはよどみ点での値。

理想気体を仮定した圧縮性流体での基本的な公式群、
$\rm a^2 = \gamma RT$

$\rm M= \frac{u}{a}$

$\rm Cp-Cv = R, Cp = \gamma Cv$

$\rm p = \rho RT$

(a:音速, R:ガス定数, γ:比熱比)

上記を踏まえて(1)式を変形すると

$\rm C_p T +\frac{1}{2} u^2 = C_p T_t$ 　…(2)

両辺をγRTで割って

$\rm \frac{1}{\gamma - 1} + \frac{1}{2} M^2 = \frac{1}{\gamma - 1} (\frac{T_t }{T})$ 　…(2)

Tt/Tについて整理すると

$\rm \frac{T_t}{T} = 1+\frac{\gamma - 1 }{2 }M^2$ 　…(3)

全温と温度・マッハ数の関係式である(3)式が導かれました。

全圧の導出（理想気体）

上流から淀み点まで等エントロピー的に圧縮したと過程すると、
等エントロピー変化の関係式より

$\rm \frac{T_t}{T}= (\frac{p_t}{p})^{\frac{\gamma - 1}{\gamma }}$ 　…(4)

(3),(4)式から

$\rm \frac{p_t}{p} = (1+\frac{\gamma - 1 }{2 }M^2)^{\frac{\gamma}{\gamma - 1}}$ 　…(5)

全圧と圧力・マッハ数の関係式(5)が導かれました。

非圧縮流体の場合、
$\rm p_t = p +\frac{1}{2} \rho u^2$ …(6)
のような形で密度、圧力、流速が分かれば全圧が求まりますが、圧縮性流体の場合には(5)のようにマッハ数が必要になるので、圧力、流速に加えて温度が必要になります。流速を直接測定するのは難しいので、ピトー管や温度計を用いて全圧、静圧や全温なり静温を計測した上で従属的にマッハ数や流速が求まる、といった計測が多いのでは無いかと思います。

マッハ数Mが非常に小さければ、そこでの温度・圧力は近似的に全温・全圧とみなせるので、流れ上流にタンクやチャンバーのような流速が非常に小さい広い領域があるような場合は、そこでの温度や圧力を流れの全温、全圧とみなす場合があります。圧縮性流体の数値解析では上流側流入条件として全温全圧を指定する場合も多いです。

間違いに気づかれた方はご指摘頂けるとありがたいです。