回転円筒の風損の計算 - 機械系技術者の雑記帳

円筒型の空間の内部で回転する円筒の流体の摩擦による風損を概算します。
ちなみに風損は英語でwindageです。

f:id:tone_akadaya:20180318172530p:plain

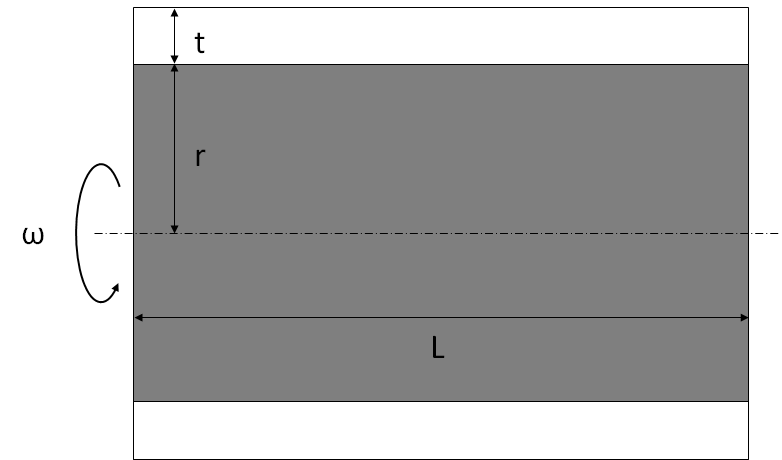
t:内外壁間のギャップ幅[m]

r:回転体の半径[m]

L:ローターの長さ

ω:回転の角速度[rad/s]

側面の抵抗

以下文献を参考にしています。なるべく以下文献を直接見て頂いたほうが良いと思います。

NASA Technical Reports Server (NTRS) - Prediction of windage power loss in alternators (文献※1)

層流の場合

内壁に働く摩擦応力τ[Pa]が求まればトルクT[N m]及び動力P[W]は

$\rm T = \tau \times (2\pi rL) \times r = 2\pi r^2 L \tau$

$\rm P=T\omega = \tau \times (2\pi rL) \times r \omega = 2\pi r^2 L \omega \tau$

によって求まるので、摩擦応力τがどのように表されるかを考えます。

ここでは円筒間の流れが層流で、且つt << rの場合を考えます。

内壁の摩擦応力をτi, 外壁τoとした場合、

内壁に掛かるトルクと、外壁に働くトルクは釣り合うので、

$\rm \tau_i \times r = \tau_o \times (r+t)$

となって一般に外壁のほうが小さいトルクになりますが、t<<rを仮定すれば、

$\rm \tau_i = \tau_o = \tau$

のように内壁と外壁に働く応力は等しくなります。

f:id:tone_akadaya:20180318174935p:plain

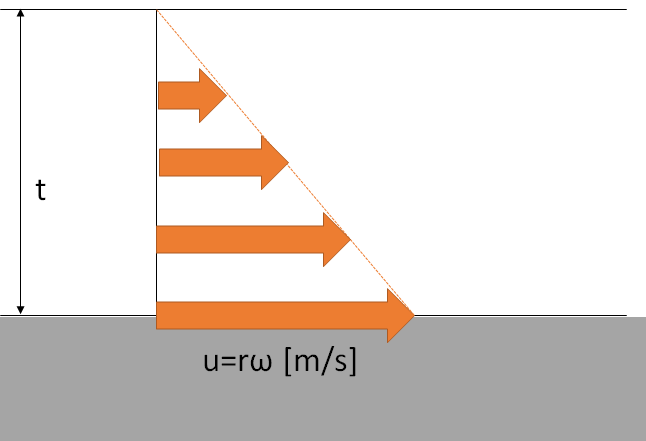
この場合、摩擦応力τは速度勾配と流体の粘性係数[Pa・s]を用いて

$\rm \tau =\mu \frac {u}{t} = \mu \frac {r \omega }{t}$ ・・・(1)

で求められます。上式のτよりトルクTと動力Pは以下の計算式で求まります。

$\rm T = 2\pi r^2 L \tau = \frac{2\pi \mu r^3 L \omega}{t}$ ・・・(2)

$\rm P=T\omega = \frac{2\pi \mu r^3 L \omega^2}{t}$ ・・・(3)

乱流の場合

乱流の場合、流体間に渦が生じて粘性力以外の運動量の交換が生まれるので、速度分布は壁面間で直線では無くなります。この場合は層流のように式(1)では摩擦応力が求められないので、摩擦応力τを摩擦係数Cdを用いて以下のように表現して、

$\rm \tau =C_d \frac {\rho u^2 }{2}$ ・・・(4)

摩擦係数Cdを求めることを考えます。

摩擦係数CdはRe数を用いた以下の式により、実測に対して良い近似が得られることが確かめられています。

$\rm Re =\frac {\rho u t }{\mu }$ ・・・(5)

$\rm \frac {1}{\sqrt{C_d }} =1.768 ln(Re \sqrt{C_d} ) +2.04$ 　・・・(6)

(ρ:流体密度[kg/m3]、u:内壁の回転速度[m/s]、μ:粘性係数[Pa・s]、t:無い外壁間の距離[m])

(文献※1参照)

式(6)はCd=[…]の形に解く（代数的に解く）のは難しいので、数値的に解く方法が一般的です。式(6)の左辺ー右辺=0になるようなCdを探すことで解となるCdを求めることが出来ます。身の回りのツールでは、エクセルのソルバー機能を使うのが簡単です。

式(6)のCdと式(4)からτを求めることで、トルクTと動力Pは以下の計算式で求まります。

$\rm T = 2\pi r^2 L \tau = \pi C_d \rho r^4 L \omega ^2$ ・・・(7)

$\rm P=T\omega = \pi C_d \rho r^4 L \omega ^3$ ・・・(8)

層流と乱流の比較

層流の場合にも式(2)を当てはめて、

$\rm \tau =C_d \frac {\rho u^2 }{2}$

Cdがどのような値を取るか考えてみると、式(1)、(5)との対応よりCdは以下で与えられることが分かります。

$\rm C_d =\frac {2}{Re }$ ・・・(9)

式 (6),(9)のCdを図示すると以下のようになります。

f:id:tone_akadaya:20180325200945p:plain

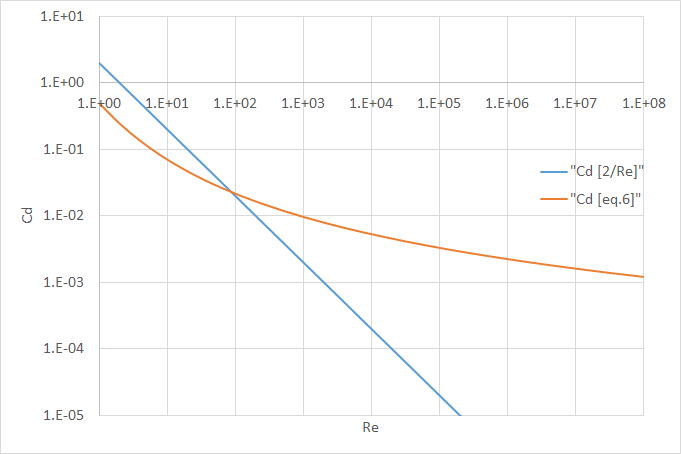
低Re数の領域では式(9)の青の系列、高Reの領域では式(6)の橙の系列になります。交差するRe=100付近で必ずしも層流から乱流に遷移するわけではありませんが、損失の概算の際には高い方で見ておけば良いと思います。乱流域では大雑把に抵抗係数が1E-2～1E-3の間になるというのが計算の際の一つの目安になると思います。

端面の抵抗

端面の円盤部分（円形の面）の抵抗です。（書きかけ）

以下参考文献。

NASA Technical Reports Server (NTRS) - Experiments on drag of revolving disks, cylinders and streamline rods at high speeds (文献※2)

間違いを見つけられた方はご指摘頂けるとありがたいです。m(_ _)m